Nシリーズの積載余剰とか速度とかの話

なんですが、その前に少し寄り道をしてチューンのお話をします。

　　チューンの増減量とは如何に決められているのか？

これを追求していくうちに速度式の正体が見えてきました、
というのがこのページの趣旨です。

• チューン量の話
  

  まず私が選んだのはジェネレータ容量のチューン量です。
  値が大きいので精密に議論できそうな気がするからです。
  （ちなみにNX以降ジェネ容量は変更されていません。）
  
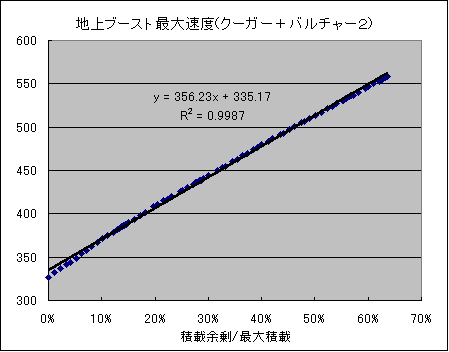
  それで下がLR全ジェネに関する元のチューンしてない量と
  フルチューンした容量とをグラフにしたものです。
  

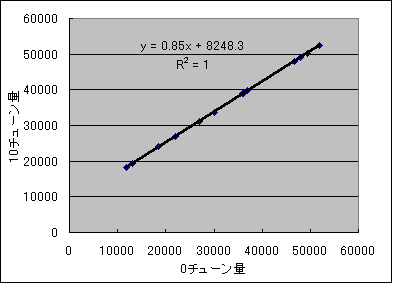  線形になってるっぽいですね。そこで
  
  　　フルチューン量＝0.85*元の量+8250＝元の量+0.15*（55000-元の量）　端数切捨て
  
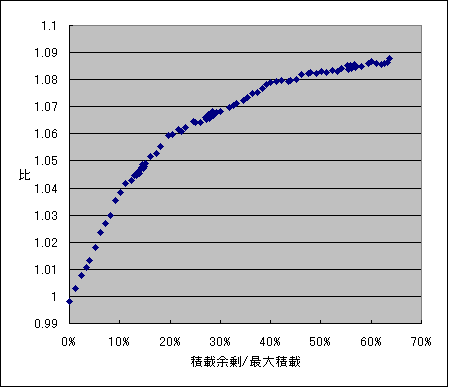
  と予測すると切捨てしない時のズレは次のようになります。
  

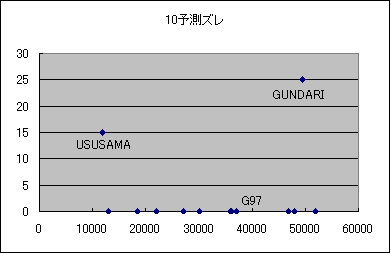  試しにFF新パーツも混ぜてみましたがその辺でズレが大きいようです。
  他は正確に０です。（つーかそうなるように決めたのですが）
  
  このような事は他のアセン部位の色々なチューン項目にも当てはまります。
  一般にLRでは、
  
  　　フルチューン増加分＝A*(B-元の量)　　端数切捨て
  　　or
  　　フルチューン減少分＝A*(元の量-B)　　端数切捨て
  
  　　　　　　（A、Bはアセン部位やチューン項目ごとに決められている量。）
  
  と書けます。（切片Bはチューンで増加する場合は元の量の一般的な値に
  比して大きめの量に、減少する場合は小さめの量に設定されています。
  これが元の量が大きければチューンしてもあまり増加しないとか、元が
  小さければあまり減少しない、とかいったことの式上での説明になっています。）
  
  残念なことに腕部照準精度のチューンでは近似的にしか
  線を引くことはできませんが、その他の項目では厳密に
  直線を引くことができます。
  
  NXではどうかというと、概ね上記の通りなのですが、まれにどう線を引いても
  ±１ぐらいズレる、といったことが生じます。おそらく式を悟られたくなかったので
  微妙にずらしてあるんだと思われます。
  NBでは例え変更されたパラメタでもチューンによる増加・減少分はNXに同じです。
  たぶん面倒くさかったのでしょう。
  FF新内装パーツでは適当に決めてあるっぽいです。ズレ大杉ですから。
  そしてLRではもう最後なので厳密に式通りにしてしまった、と想像できます。
  
  さてジェネの話に戻ります。
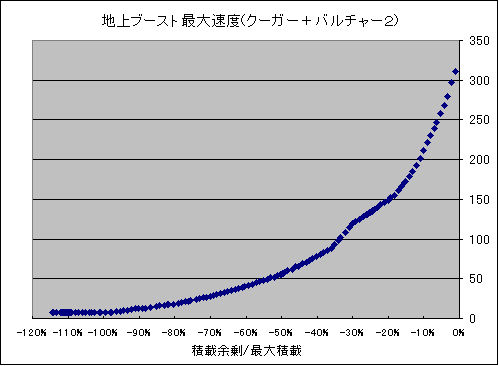
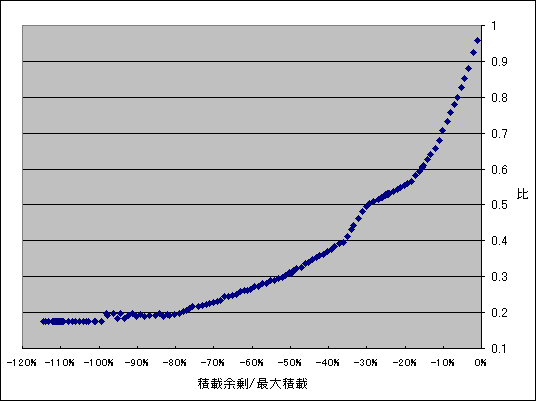
  今度はジェネレータを１つ選び、少しずつチューンして増加する様子を見てみます。
  ジェネはORCHIDです。やはり量が大きいからです。
  

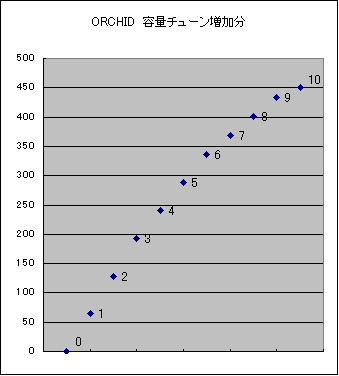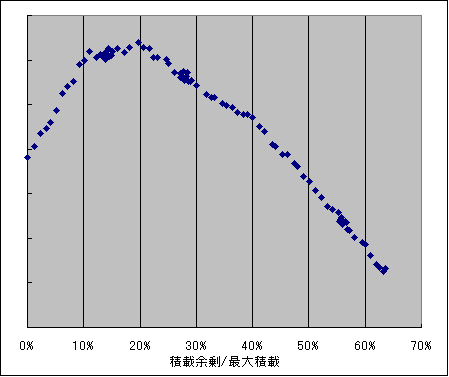
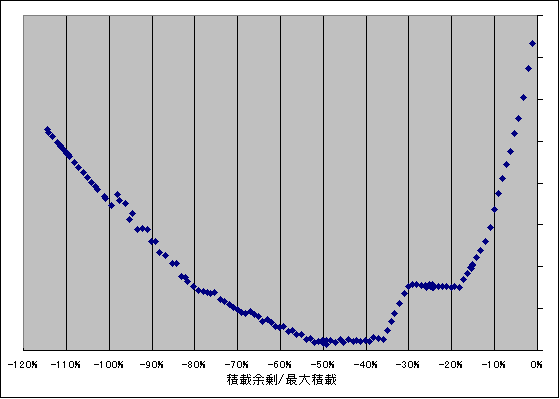
  曲線っぽく見えますが、形をはっきりさせるために、
  原点から１０チューン点まで線を引いて差を取ってみます。
  

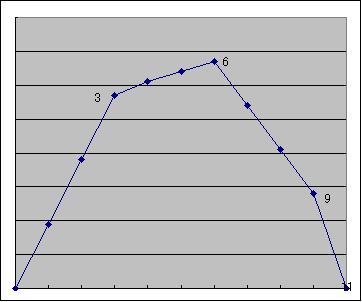  どういうわけか曲線みたいなのが折れ線みたくなってしまいました。
  折れているのは３と６と９です。
  
  折れている点の値はどのようにして与えられているのでしょうか？
  LR全ジェネについて元の量と３チューン量とをグラフにしてみます。
  

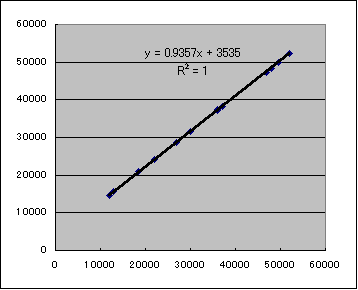  また線形になってるっぽいですね。そこで
  
  　　３チューン量＝0.9357*元の量+3536.4　端数切捨て
  
  と予測すると切捨てしない時のズレは次のようになります。
  

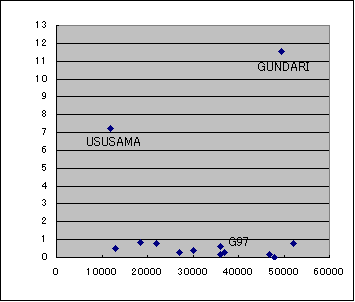  再びFF新パーツを入れてみましたが、またそこでズレが生じてますね。
  他は１未満です。
  
  ところで上の３チューン式の係数を少しズラして
  
  　　３チューン量＝元の量+{0.15*（55000-元の量）}*3/7　端数切捨て
  
  としてもまたこれも成り立ちます。これは次のようにも書けます。
  
  　　３チューン増加分＝10チューン増加分*3/7　端数切捨て
  
  これを試してみると切捨てしない時のズレがＦＦ新パーツも含めて
  全て１未満に納まってしまいます。
  

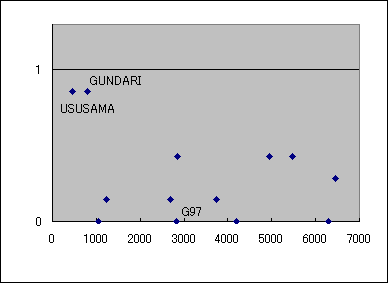  つまり10増分と元の容量とは必ずしも何らかの関係にあるわけではないし、
  3増分と元の容量でもそうなのだが、10増分と3増分とは比例関係にある？
  のだと。そこでこちらの式の方がチューン量を記述する上でより基本的なもの
  と考えられます。
  
  さらに６でも９チューンでも上手く比例係数を選ぶことができます。
  
  　　６チューン増分＝１０チューン増分*３/４　端数切捨て
  　　９チューン増分＝１０チューン増分*２７/２８　端数切捨て
  
  これらはやはりFF新パーツでも成り立ちます。
  実は全チューン項目（腕照準精度以外）で成り立ちます。
  NXでもNBでもFFでもです。
  １０チューン量が０チューン量との線形式上に乗っているかどうかに無関係です。
  
  では３・６・９の間ではどうなっているのでしょうか？
  様々な部位の色々な項目について調べてみたのですが、
  どうやらここは直線になっていると見て差し支えないようです。
  つまり（腕照準精度以外では）、
  
  　　１・２・３チューン増減分＝１０チューン増減分*１/７・２/７・３/７
  　　３・４・５・６チューン増減分＝１０チューン増減分*３/７*４/４・５/４・６/４・７/４
  　　６・７・８・９チューン増減分＝１０チューン増減分*３/４*２１/２１・２３/２１・２５/２１・２７/２１
  　　　　いずれも端数切捨て
  
  と書けるっぽいらしいのです。前にグラフで見た時にこれは折線のように
  見えるといいましたが、本当にそうなっていました。
  
  まとめ。
  
  　　腕部照準精度以外では、
  　　０チューン量と10チューン量を与えればその間のチューン量も次のように求まる。
  
  　　　　ｄチューン増減分＝１０チューン増減分*Ｔ（ｄ）　端数切捨て
  
  　　　　　　ただしＴ（ｄ）は次の点で決まる折線
  　　　　　　　　Ｔ（０）＝０　Ｔ（３）＝３/７　Ｔ（６）＝７/４　Ｔ（９）＝９/７　Ｔ（１０）＝１
  
  　　１０チューン増減分は概ね０チューン量の一次式を目安に
  　　決められているが、（LR以外では）厳密ではない。
  
  長々と話をしましたが、ようするに折れ線を使って曲線のように見せかけている、
  という点だけ理解していただければ結構です。
  

• 積載余剰問題の話
  

  さていよいよ本題に入ります。ブースト速度式の話です。
  
  それで下が足とブースタを固定し、上半身を軽く（積載余剰を大きく）させた時の
  地上ブースト最大速度の実測値です。
  

  直線っぽく見えます。それでそれらしい直線（kouyou氏言う所の
  基準式にあたる）を取ってそれとの比を取ってやる。
  

  曲線っぽくなってしまいました。
  実はOB速度、歩行速度、旋回速度、被弾安定性、ブレード(光波)威力でも
  同様の線が見受けられます。この線がどんな関数か分からない、
  それがいわゆる積載余剰の問題というやつです。
  
  ところがこれを分かりやすい形に変形することができます。
  特に意味のない適当な直線（今は原点から適当な傾きで取ります）を
  引っぱって差を取ってやると、
  

  折れ線っぽくなってしまいました。チューン量と同様の事象が起きているわけです。
  折れてる所は多分１０、２０、４０％です。（細かく測定すると実は５、８％あたりでも
  ポキッと折れています。）
  
  まぁここでは折れた直線とまでは断定しませんが、少なくとも途中で法則が変化している、
  例え直線でなかったとしても各々の区間で線形近似が有効である、と期待できます。
  
  私は既にネクサスの頃に積載余剰曲線は実は折れた線ではないかと思っていましたが、
  その仮定の下に解析するのは非常に手間がかかるし、したとして満足な成果が得られるか
  自信が持てませんでした。しかし2005年秋頃にチューン量の正体が分かってきて、それと
  同様の仕掛けが施されているな、という確信が得られてやっとやる気が出てきたわけです。
  
  次に気になるのが重量過多時ですね。グラフにするとこうなります。
  

  普通に減衰する曲線のようです。けれどもここで非重量過多時の調査で
  初めに使った基準直線を使って無理やり比を取ってみます。
  

  やはり分かりにくいですから、また非重量過多時と同様に適当な直線との差を取って
  変形し、見やすくしてみましょう。
  

  と、言うわけでこれも折線っぽくなってしまいました。まとめると
  
  　　最大速度＝基準式ｘ折線
  
  です。基準式は最初に満載時の速度式として発見されました。それを
  非満載時にも延長適用したわけですが、これは機体全重量の線形式です。
  つまり
  
  　　最大速度＝線形式（全重量）ｘ折線（積載余剰/最大積載）
  
  の係数を決めていけばよいわけです。
  
  ところがここに１つの問題があって、折線関数が全ての脚で共通である、といった
  保証が実はどこにもないのです。単純に色々の足の折線関数を比較すればいい、と
  お考えになられるかもしれませんが、線形部分と折線部分とは測定値から同時に決定
  されるべきものであって、両者は一方のズレに対して非常にセンシティブです。一方
  だけをひょいと取り出せるようなわけにはいきません。
  そこで私は旋回速度のガレージ表示に注目しました。これは速度グラフとは折れ点
  の位置が異なり、また、ガレージ表示自体にも誤差があるわけですが、誤差はただ
  １つの折線の周りに一様に分布しているように見受けられます。そこで折線関数は
  全脚部について共通であると仮定して測定に入ります。（折れ点のＸ座標が１０、
  ２０、４０％と美しい所からも正しいように思われました。）
  
  できるだけ多くの脚部、ブースタについて折れ点での速度を測定し（折れ点の間が
  直線かどうかは未知だからです）、それをエクセルに入力、式係数を細かく動かします。
  そして遂に全ての折れ点で理論値と計測値を合致させることに成功したのです。
  
  そして折直線仮定のもとに式を作り、スクリプトにしました。
  私はいろいろな数字を入れて実際の値と比べてみましたが、誤差は±１以内に収まって
  いるようです。めでたしめでたし。
  でもよくよく考えてみると３シリーズでは
  
  　　最大速度＝一般関数（全重量）　　　　　　（積載未満）
  　　最大速度＝折線（積載余剰/最大積載）　（重量過多）
  
  であったのですが、これを積載以上・以下によらず全区間で成り立つ関数となるように
  すればＮシリーズ速度式の出来上がりというわけで、正体が分かってしまうと単純な話です。
  
  （この式はLR・FF・NBで成り立ちますが、NXでは折れ点の位置が異なり成り立ちません。）